Logo

4.1 Finite Property of $c$

Our previous discussion has shown that the power parameter $c$ of the "$h$" function has a finite property even if it approaches infinity. Theoretically, we can compute the gamma function with arbitrary precision by increasing the value of $c$, but this result will not be exact unless the base parameter $s$ is a positive integer or half-integer. Both cases are exceptional since $\Gamma \left( 1 \right)$ and $\Gamma \left( \tfrac{1}{2} \right)$ are the only cases, among all of $\Gamma \left( s \right)$ in which $s\in \left( 0,1 \right]$, for which the result can be exactly proved. The idea of the factorial product, therefore, can be applied to the natural numbers and half integers. For the remaining cases, we need a numerical analysis to estimate the degree of error resulting from the choice of $c$.

Computationally, the finite property of $c$ means that we can bring a considerably larger number $C$ to replace the infinite integral limit. But how large a $C$ qualifies as "considerably larger"? We investigate this question by evaluating numerical precision of the "$h$" factorization methods. Our target of analysis is $\Gamma \left( s \right)$, where $s=0.1,0.2,\cdots ,1$. Starting from $C=10$, we increase $C$ by 10 until 100 and round the result to significant decimal places. As Table 1 shows, all numerical errors pass the default precision level in Matlab's environment (15 digits) when $C$ is $40$. As we continue increasing the value of $C$, the precision level increases in a linear fashion. Generally, each increase of $C$ by $10$ will elevate the precision level by four decimal places. When $C$ is set at 100, the precision level reaches 43 or more significant decimal places. In addition, the precision level also differ slightly when we vary the input argument of $\Gamma \left( s \right)$ from 0.1 to 1. Apparently, the precision level is higher when the base parameter $s$ is closer to 0, and in other instances, it is slightly lower.

For a practical standard, $C$ can be set to the default precision level of a user's computing environment. The author suggests $C=20$ (at least 8 significant digits) should serve the computational purpose well. Nonetheless, since the "$h$" factorization method can provide a result with arbitrary precision, readers can determine their own setting of $C$ according to the precision level they wish to achieve.

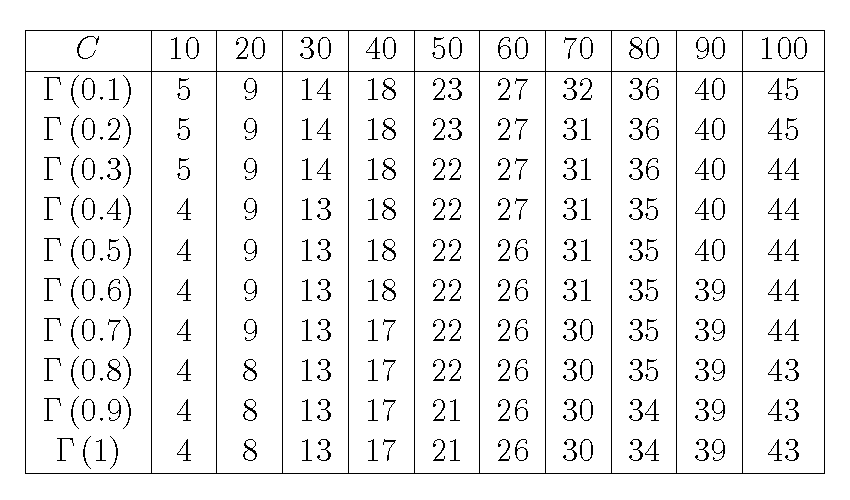
Table 1: Total Number of Significant Digits by Varying C

Download [full paper] [supplementary materials] [.m files] [technical note]